Harmonic Analysis
A harmonic analysis is performed to determine the response of a piping system to sinusoidal loads. Harmonic forces can arise from unbalanced rotating equipment, acoustic vibrations caused by reciprocating equipment, flow impedance, and other sources. These forces can be damaging to a piping system if their frequency is close to the piping system’s natural frequency, thereby introducing resonant conditions. The equation of dynamic equilibrium associated with the response of the structure subjected to harmonic forces is:
 |
(27)
|
where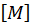 
= diagonal mass matrix
= diagonal mass matrix
= damping matrix
= stiffness matrix
= displacement vector
= velocity vector
= acceleration vector
= frequency of the applied force
= time
= maximum magnitude of the applied forceIt is feasible that multiple harmonic loads may be applied simultaneously at different locations of a piping system. More complex forms of vibration, such as those caused by the fluid flow, may be considered as superposition of several simple harmonics, each with its own frequency, magnitude, and phase.
A harmonic analysis uses the results from the modal analysis to obtain a solution. A single damping factor is used for all modes.
First, the maximum response for each harmonic load is obtained separately. Then, the total response for multiple simultaneous harmonic loads is determined by combining the individual responses. The combination method may be specified as the Root Mean Square (RMS) or Absolute Sum. Even in the case of a system with a single harmonic load, the said combination is always carried out, so that the resulting solution becomes an “unsigned” case. For an unsigned case, the actual values for displacements, element forces and moments, etc. computed internally by CAEPIPE prior to such combination can be +ve or -ve for the dynamic event. After the combination, the resulting values become “unsigned”.