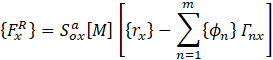Missing Mass Correction
In dynamic analysis using modal superposition, usually an approximate solution is obtained because only a limited number of modes is considered. (For seismic analysis, typically all modes up to 33 Hz). The errors in pipe displacements and stresses are usually small because they are affected relatively little by high modes. The error in support loads may be substantial because the influence of higher modes on support loads can be important. In stiff piping systems with few low frequency modes, stresses may also be affected significantly.
Using limited number of modes results in some mass of the system being ignored. The distribution of this “missing mass” is such that the inertia forces associated with it will usually produce small displacements and stresses. However these forces will often produce significant support loads, and in stiff systems can produce significant stresses.
A correction can be made by determining the modal contributions to the mass of the system and obtaining the “missing mass” as the difference between these contributions and the actual mass.
The inertial force vector for the nth mode is given by
 |
(1)
|
Where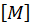 
= diagonal mass matrix
= diagonal mass matrix
= acceleration vector
= circular frequency
= mass normalized eigenvector
= modal displacement for mode nFor X seismic excitation
 |
(2)
|
Where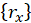 
= displacement vector due to a unit displacement in the X direction
= displacement vector due to a unit displacement in the X direction
= spectral acceleration for the nth mode for excitation in the X direction
= mass participation factor in the X direction for mode nLet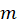 
= number of modes used in analysis
= number of modes used in analysis
= total number of modesIf it is assumed that the higher modes: m+1 through N are in phase and have a common spectral acceleration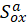
(conservatively taken as the maximum spectral acceleration after the mth mode), the total inertial force contribution of these higher modes (also known as “Rigid body force” or “Left out force”) is
(conservatively taken as the maximum spectral acceleration after the mth mode), the total inertial force contribution of these higher modes (also known as “Rigid body force” or “Left out force”) is
 |
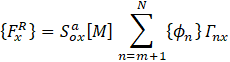(3)
|
It can be shown that
 |
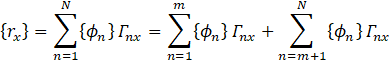(4)
|
|
|
Substituting from (4) for the summation in (3)
Note that there will be missing mass inertia forces in the Y and Z directions, in addition to the X direction, for X excitation.
The missing mass force vectors for the Y and Z directions are similarly calculated. The response to each of these three force vectors is calculated and these additional response vectors are combined with the responses of the first “m” modes.
This feature is currently not available for Time History, Multi-Level Response Spectrum and Harmonic analyses.
The above described method is based on the technical paper by Powell. See below for details.
Powell, G.H. “Missing Mass Correction in Modal Analysis of Piping Systems.” Transactions of the 5th International Conference on Structural Mechanics in Reactor Technology. August 1979: Berlin, Germany.