Direction
Direction is required for several items such as Pump, Compressor, Turbine, Nozzle (for vessel axis), Limit Stop, Skewed restraint, Elastic element and Hinge joint.
The axis or the orientation of an item (listed above), is called the direction vector which is described in terms of the vector’s global X, Y and Z components.
The angles the vector makes with the X, Y and Z axes are called Direction angles, whose cosines are called Direction cosines (or global X, Y and Z components used in CAEPIPE).
There are two methods of computing the X, Y and Z components.
First method: When you know the direction angles (see examples 1, 2 and 3).
Example 1: Vertical Vessel
Assume a vertical vessel with axis in the Y direction, and a, b, g as the direction angles the axis of the vessel makes with global X, Y and Z axes.
The angles are a = 90°, b = 0° (since axis is parallel to Y axis) and g = 90° .
So, the direction cosines or X, Y and Z components are
X comp = cos (a = 90°) = 0,
Y comp = cos (b = 0°) = 1,
Z comp = cos (g = 90°) = 0.
For Z vertical: X comp = 0, Y comp = 0 and Z comp = 1.
Example 2: Limit Stop at 45° from the X-axis in the X-Y plane
For a limit stop whose axis is oriented at 45° from the X-axis in the X-Y plane, the angles are a = 45°, b = 45° and g = 90°.
So, the direction cosines or X, Y and Z components are
X comp = cos (a = 45°) = 0.70711,
Y comp = cos (b = 45°) = 0.70711,
Z comp = cos (g = 90°) = 0.0
Example 3: Hinge axis at 30° from the Z-axis in the Y-Z plane
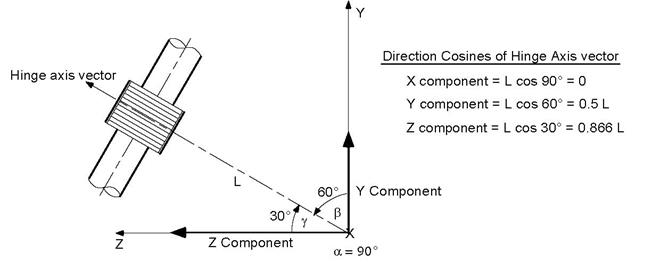
From the above figure, we have the angles α = 90°, β = 60° and γ = 30°. Assuming L = 1 (or any length), the direction cosines or X, Y and Z components are
X comp = cos (α = 90°) = 0.0,
Y comp = cos (β = 60°) = 0.5,
Z comp = cos (γ = 30°) = 0.866
Example 4: Skewed Support
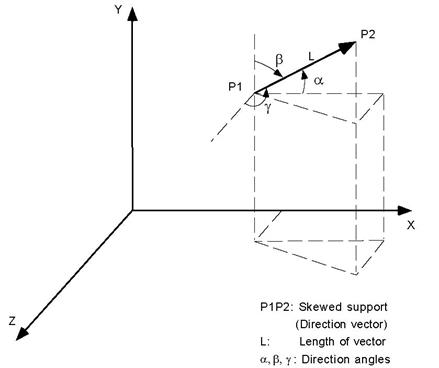
Assume that we have a skewed support along P1P2 (which is the direction vector) shown in the figure above, Assume that the coordinates of these two points are P1 = (12’,12’,12’) and P2 =(15’,16’,14’).
Let us calculate this vector’s global X, Y and Z components. There are two methods here
Short method
X comp = (X2 − X1) = (15 − 12) = 3
Y comp = (Y2 − Y1) = (16 − 12) = 4
Z comp = (Z2 − Z1) = (14 − 12) = 2
Long method
First, let us calculate the length of the vector, L.
The angles α, β and γ which the vector makes with the global X, Y and Z axes are called the Direction angles of the vector; The cosines of these angles are called Direction cosines.
The direction cosines are
X comp = cos α = 0.55709, Y comp = cos β = 0.74278, Z comp = cos γ = 0.37139
For information, the direction angles are α = 56°8’0”, β = 42°1’0” and γ = 68°11’0”.
To verify the results, the sum of the squares of the direction cosines must be 1.0. Thus,
cos2α + cos2β + cos2γ = 0.5570922 + 0.7427822 + 0.3713922 = 1.0