Comments on Pressure Expansion

Tip of the Month April 2002

In CAEPIPE Version 5.1E (Mar 14, 2002) a change to the program states:

Presently pressure expansion (Bourdon effect) is treated as thermal expansion and applied to expansion (T) and operating (W+P+T) load cases. If an environment variable BOURDONP is set (i.e. set BOURDONP=y), pressure expansion is not treated as thermal expansion (i.e. pressure expansion is treated as pressure expansion and applied to sustained (W+P) and operating (W+P+T) load cases).

Treating a pressure caused stress as a thermal expansion-like stress may seem incorrect to some analysts, but treating pressure expansion as a load similar to thermal expansion is the correct interpretation of the type of load and the failure mode related to that type of load. Pressure expansion causes displacement (secondary) stresses and leads to a fatigue failure. Hoop pressure (PD/2t) and longitudinal pressure (PD/4t) type stresses are sustained (primary) stresses, but pressure expansion, if the piping is unrestrained would not cause any displacement (secondary) stresses. Restraining the pipe, as in introducing more than one anchor or an intermediate support opposed to the direction of pressure expansion, causes stresses from the introduction of that restraint. A simple illustration is shown below:

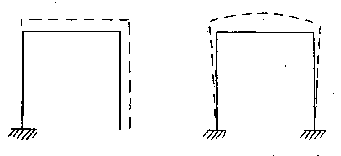
Shown are two weightless piping layouts. Note the layout on the left has a single anchor and when pressurized will expand as shown to the dashed line configuration. Sustained load stresses due to hoop and longitudinal pressure exist, but no additional stresses due to pressure expansion exist. However, note what happens when an additional anchor is introduced, restraining the piping pressure expansion in the right hand layout. The deformed shape is indicative that stresses exist due to the "restraint of free end displacement" in addition to the hoop and longitudinal pressure stresses. These pressure expansion stresses are displacement (secondary) stresses and should be treated in a similar manner to thermal expansion stresses.

Note also, the Bourdon effect, which tries open elbows or curved members when such are pressurized, is a pressure expansion effect and should be treated the same way that simple pressure expansion as discussed above is, i.e., the Bourdon effect causes displacement (secondary) stresses.

Further note that Pressure expansion was usually ignored prior to the use of computer aided analysis techniques because most piping analyzed was metallic, typically steel, piping. It was ignored because the amount of pressure expansion was normally small compared to thermal expansion, i.e., typically less than 10 percent. However, with low modulus materials, such as nonmetallics (plastics), the amount of pressure expansion can be significant and may need to be considered in the analysis of piping systems made from such materials.

Editor's Note: Since version 3.32 (4/22/1992) CAEPIPE has been treating pressure expansion as a secondary load (similar to thermal expansion) and applying it to thermal and operating load cases. This is the default behavior of CAEPIPE (even now).

However, a few users want to treat pressure expansion as a primary load and apply it to the sustained and operating load cases because finite element programs and other piping programs do it this way. Starting v5.1E, these users (with some effort by setting an environment variable) can alter CAEPIPE's behavior (i.e., treat pressure expansion as a primary load) to suit their needs. Please see the second para. above in this article for how to set the variable.

Author: Mr. Ron Haupt, P. E., of Pressure Piping Engineering (www.ppea.net) is a member of several piping code committees (B31, B31.1, B31.3, BPTCS, and others). He consults with us in the capacity of Nuclear QA Manager.

Limit Stops in Dynamic Analysis

Tip of the Month May 2002

Question: How are limit stops handled in dynamic analysis (response spectrum, time history, harmonic)? We noticed that the displacements in the results for dynamic cases could be higher (e.g., 108.45 mm) than those input for limits at the limit stops (e.g., 50 mm and -70 mm). Results indicate that a limit stop has "not reached." Please explain.

Reply: Dynamic analysis in Caepipe is performed using mode superposition which is a linear process whereas analysis of limit stops is a nonlinear process. It is not possible to include nonlinearities in dynamic analysis. As an approximation only, nonlinearities are "sort of" indirectly included in dynamic analysis by using the stiffness associated with them from the first operating case (W+P1+T1) during modal analysis.

In the case of limit stops, if a limit is reached during the first operating case, then the associated stiffness is used in modal analysis. If a limit is not reached, then the limit stop is ignored in modal analysis. Even if a limit is reached and the stiffness is used in modal analysis, it is still not possible to use the actual limits (upper and lower) in modal analysis.

In the example mentioned, the limits are not reached in the first operating case. This status is used in modal analysis and subsequently in dynamic case analysis. So, in effect, this limit stop is not used.

Tip of the Month June 2002

There is no tip for this month.