Software Solutions
- CAEPIPE
- CAEPIPE 3D+
- checkSTRESS
- dataTRANSLATORS
- HOTclash
- PEXit
- Pricing Request
- Download Free Evaluation
- Download CAEPIPE 3D+
- Download Free Review Module
- Customer Support
Engineering Services
- Design and Engineering
- INFOplant™ System
- Engineering Management
- List of Projects
- Project Gallery
- Project Videos
Learn More
Company Information
Tips January - March 1999
Estimating Relief Valve Discharge Force for CAEPIPE
Relief valves are used in piping systems to provide an outlet for those situations when pressure builds up beyond that desired for safe operation.
The escaping fluid creates a jet force which is transferred through the pipng system. This force must be resisted by the pipe supports if the pipe is incapable of resisting the force internally. The magnitude of the force is usually given by the valve manufacturer. It can be easily calculated however, for those situations where the valve vents to the atmosphere.
ANSI B31.1 recommends the following method for calculating this force.
F = DLF ( MV/32.2 + PA) (English units)
F = DLF ( MV+ PA/10^6) (SI units)
V = SQRT(50,113 (ho - a)/(2b - 1) ) (English units)
V = SQRT(2.0085 (ho - a)/(2b - 1) ) (SI units)
P = (M/A) (b - 1)/b SQRT(48.33 (ho - a)/(2b - 1)) - Pa (English units)
P = (M/A) (b - 1)/b SQRT((1.995 x 10^12) (ho - a)/(2b - 1)) - Pa (SI units)
where
F = Discharge force (lb., N)
DLF = Dynamic load factor (dimensionless), see discussion below
M = Mass flow rate from valve x 1.11 (lbm/s, kg/s)
V = Fluid exit velocity (ft/s, m/s)
P = Static gauge pressure at discharge (psi, N/m^2)
A = Discharge flow area (in^2, mm^2)
Pa = Atmospheric pressure (psi, N/m^2)
ho = Stagnation enthalpy of pipe fluid (Btu/lbm, J/kg)
a, b are as given below:
| a | b (dimensionless) | ||
| Steam Condition | Btu/lbm | J/kg | |
| Wet, <90% quality | 291 | 675,411 | 11 |
| Saturated, > 90% quality | 823 | 1,910,183 | 4.33 |
| Superheated | 831 | 1,928,751 | 4.33 |
Comments on Flexibility Analysis
The American Society of Mechanical Engineers (ASME) B31 Code for Pressure Piping was developed with the expectation that piping system designers would be familiar with the concept of flexibility. For this reason the B31 Codes never described or discussed in any depth the intention of either performing a flexibility analysis or the results expected therefrom. The flexibility equation, also referred to as the thermal expansion or displacement stress equation,
SE = SQRT(Sb^2 + 4 St^2)
was incorporated into the 1955 Edition of B31.1 in Section 6, Chapter 3, Expansion and Flexibility. In 1955 the B31.1 book had different sections for different applications, i.e., Section 1 for power piping, Section 2 for industrial gas and air piping, Section 3 for refinery and oil transportation piping, Section 4 for district heating piping, and Section 5 for refrigeration piping. But prior to 1955, in 1952, the B31.8 Gas Transmission and Distribution Piping book was published, initiating the publication of the separate applications books we have today, i.e., B31.1 Power Piping, B31.3 Process Piping, B31.4 Liquid Transportation Piping, B31.5 Refrigeration Piping, and B31.9 Building Services Piping. Each of these applications books, when published, incorporated the flexibility equation following a B31 code model outline developed in the 1950's. B31.8 also incorporated the flexibility equation even though B31.8 did not follow the model outline owing to the fact that B31.8 was published prior to the development of the B31 model outline.
The allowable flexibility stress-range for the 1955 Edition of B31.1 was based on the expectation of elevated temperature operation and ductile behavior, and first introduced the concept of self-springing or shakedown to ASME pressure component design. Generally, the flexibility allowable stress-range was permitted to approach two times yield. However, the pipeline codes, B31.4 and B31.8, never adopted the twice yield allowable stress-range (shakedown) concept because it was expected that pipelines would experience nonductile behavior. Code revisions over the years since 1955 have not served to clarify the concept of flexibility and in many ways have obscured it. For example, B31.1 deleted a stress equation which implied the methodology typically used for flexibility design.
The purpose of performing a flexibility analysis is to determine that, barring interferences and assuming a supportable geometry, the anchor-to-anchor piping configuration (layout) is acceptable. Adequate flexibility is required to avoid an expansion (or contraction) induced fatigue failure and to limit anchor loads on equipment. A flexibility analysis typically (and traditionally) evaluates the range of stresses encountered by piping system service startup and shutdown. It is generally assumed that the startup-shutdown stress-range will bound the other thermal expansion or displacement stress-ranges. The piping flexibility is evaluated between equipment and structural anchors without locating any intermediate supports. Weight stresses, then, would not be known. It is presumed that the intermediate supports for weight and other loads can be added after determining that a piping system has adequate flexibility without significantly increasing the flexibility stress-ranges. This is reflected in the circa. 1955 B31 books having an allowable thermal expansion stress-range
SA = f(1.25Sc + 0.25Sh)
and permitting an additional thermal expansion stress-range allowance of Sh - SL, when the stresses due to weight and other sustained loads, SL, were known.
After the flexibility analysis has determined that the piping has adequate flexibility, using the allowable thermal expansion or displacement stress-range, SA, then span tables and/or engineeringjudgement is used to locate intermediate supports for weight and other loads. If the thermal displacements at a proposed support point are negligible (i.e., very small), then a rigid support can be located at that point. If the vertical thermal displacements are significant at locations where weight supports are proposed, springs (variable or constant) can be used. If the lateral thermal displacements are significant at locations where lateral supports are proposed, gapped supports usually can be used. By use of support types that offer minimal restraint throughout the startup-shutdown excursion, the flexibility stress-range is not significantly increased and could be expected to be bounded by the additional thermal expansion allowance, Sh - SL. (Editor's note: Sh - SL is available in CAEPIPE as an Analysis Option (under Code) "Use liberal allowable stresses," for certain piping codes).
The entire flexibility design and analysis process assures that the effects of fatigue due to thermal expansion, or more generally the restraint of free-end displacements, are minimized. However, some caution in performing the flexibility analysis is necessary to see that other frequently occurring normal and abnormal operating condition stress-ranges do not envelope the startup-shutdown stress-range or to see that supports do not unduly restrain the load induced expanding (or contracting) piping system.
Author: Mr. Ron Haupt, P. E., of Pressure Piping Engineering (www.ppea.net) is a member of several piping code committees (B31, B31.1, B31.3, BPTCS, and others). He consults with us in the capacity of Nuclear QA Manager.
Calculating the Design Earthquake Load Coefficient (g-load) for CAEPIPE
Update: As this method is from an older edition of A58.1, we recommend that you refer to ASCE-7, 2002 edition for the latest guideline for calculating g-loads.
Piping should be designed for earthquake-induced forces. Either ANSI A58.1 or the Uniform Building Code (UBC) may be used for calculating the g-load (or static seismic coefficient).
The following is a simplified method based on ANSI/ASCE A58.1-1988 ("Minimum Design Loads for Buildings and Other Structures"). Piping is assumed to be equivalent to equipment thus giving a force coefficient, Cp as 0.3 (Table 25).
For the proper method:
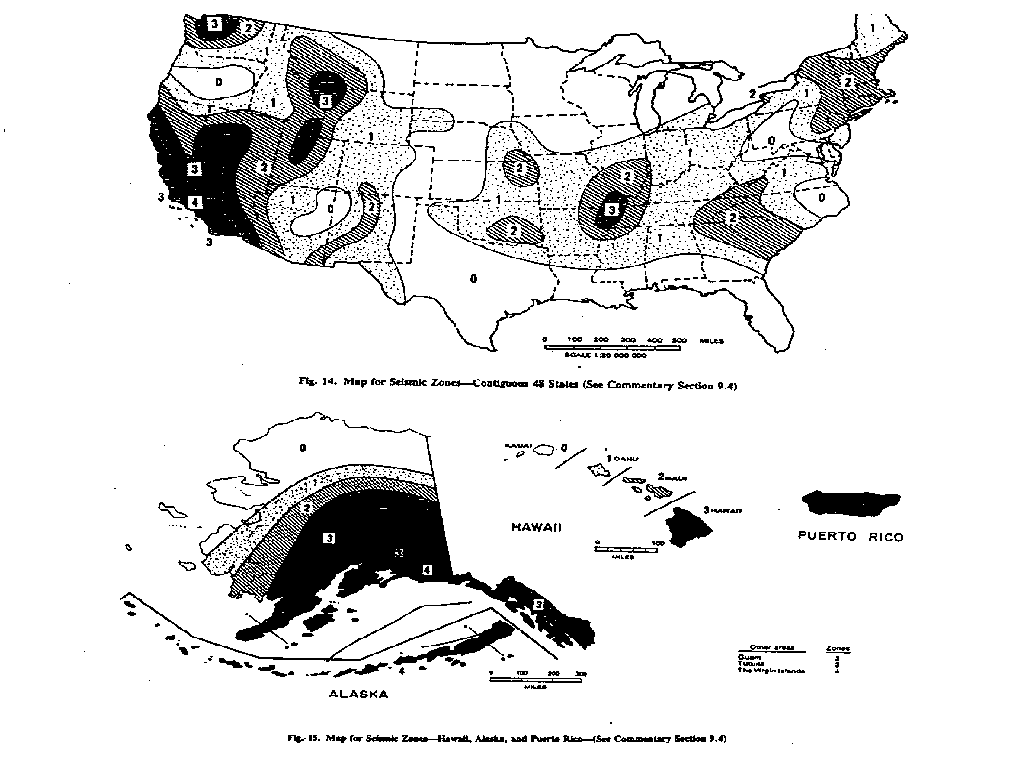
1. First, based on the map below (Contiguous 48 States+Alaska/Hawaii/Puerto Rico), identify the seismic zone and its corresponding coefficient (Z).
| Seismic Zone Coefficient | Z |
| 4 | 1.0000 |
| 3 | 0.7500 |
| 2 | 0.3750 |
| 1 | 0.1875 |
| 0 | 0.1250 |
2. Determine the Importance Factor, I.
| Type of piping Factor | I |
| Piping required in an emergency or piping with contents representing significant hazard to human life | 1.5 |
| Other piping | 1.0 |
3. Calculate the g-load as (0.3*Z*I). The equation is
Fp = 0.3*Z*I*Wp, where
Fp = Design Inertia force, and
Wp = Weight of piping including insulation and contents.
Assumptions and Exclusions:
1. Earthquake restraints may be omitted from the following installations:
a. Gas piping less than 1 inch inside dia.
b. Piping in boiler and mechanical rooms less than 1.25 inch inside dia.
c. All other piping, except that containing hazardous fluids, less than 2.5 inch inside dia.
2. Individual hangers less than 12 inches in length may be considered as seismic restraints.
Example:
For a power plant required to operate in an emergency, located in Anchorage, Alaska, calculate the design earthquake load coefficient for piping required to operate the plant.
1. From the map below, seismic zone is 4, from the table above, corresponding coefficient is 1.0.
2. For piping required to operate in an emergency, the Importance factor is 1.5.
3. Calculate the coefficient,
Fp = 0.3*1.0*1.5*Wp
Fp = 0.45*Wp
The coefficient, 0.45, needs to be applied independently in the desired horizontal/vertical directions. See map below for US seismic zones.
How does CAEPIPE analyze internally?
CAEPIPE computes the Design inertia force for each direction and applies it as an occasional load. From the example above, assume we applied 0.45g in X, Y and Z directions. CAEPIPE internally applies an X acceleration (of 0.45g) first and solves the case. This procedure is then applied independently to the accelerations in Y and Z directions.
The above procedure results in three sets of solutions (displacements, element forces and moments, and support loads) to accelerations in X, Y and Z directions, which are typically combined in some manner. In CAEPIPE, two directional combination methods are available: SRSS (Square root of sum of squares) and ABS (Absolute). The SRSS summation method employed in Acceleration (static seismic) load case and other simplified dynamic analysis methods, such as response spectrum method, is statistically based.
In the SRSS method, displacements, element forces and moments, and support loads from the three X, Y and Z accelerations are squared individually and added. The square roots of these respective sums are the displacement, element force and moment, and support load at the given node. In the ABS method, all absolute values of displacements, element forces and moments, and support loads are added to get the total displacement and support load. The resulting stresses are added to Sl (Sustained stress) and shown under Occasional stresses (Sl+So).